磁镜的磁场位形模拟

系统：Windows 10 专业版 1903
matlab版本：Windows版 2018a

使用说明

详细的推导过程见这篇文章，程序需要用到这篇文章中的 magnetic.m 程序，请将它与下面的程序放在一个文件夹下。 Simple_Mirror_3D.m 用来计算模拟磁镜的三维磁力线分布。Simple_Mirror_2D.m用来模拟磁场的二维磁力线分布，在模拟二维磁力线分布时，线圈半径取1.0m。

程序

Simple_Mirror_3D.m

tic;clc;clear;
%c0:u0/2pi,I:线圈电流(A),R:线圈半径(m),L:线圈间距(m),dl:步长
c0=2e-7;I=1e6;L=2.0;R=0.2;dl=0.001;
x=[];y=[];z=[];
r=[0.01;0.02;0.05;0.1;0.2;0.3;0.4;0.5];r=[-r;r];
for theta=0:30:180
    for j=1:length(r)
        for pm=-1:1
            for i=1:600    
                x(1)=r(j)*cos(theta*pi/180);y(1)=r(j)*sin(theta*pi/180);z(1)=0;%磁力线起点
                [Bx1,By1,Bz1]=magnetic(c0,R,I,x(i),y(i),z(i)+L/2);%线圈1产生的磁场
                [Bx2,By2,Bz2]=magnetic(c0,R,I,x(i),y(i),z(i)-L/2);%线圈2产生的磁场
                Bx=Bx1+Bx2;By=By1+By2;Bz=Bz1+Bz2;
                B=Bx^2+By^2+Bz^2;
                x(i+1)=x(i)+Bx/B*dl*pm;
                y(i+1)=y(i)+By/B*dl*pm;
                z(i+1)=z(i)+Bz/B*dl*pm;
            end
            subplot(121);plot3(x,y,z,'b-');hold on;box on;
            if theta==0;
                subplot(122);plot(x,z,'b-');hold on;
            end
        end
    end
end
%画线圈1
h=-1;t=0:0.1:(2*pi);t=[t,0];
plot3(0+0.2*sin(t),0+0.2*cos(t),h*ones(size(t)),'LineWidth',4)
%画线圈2
h=1;t=0:0.1:(2*pi);t=[t,0];
plot3(0+0.2*sin(t),0+0.2*cos(t),h*ones(size(t)),'LineWidth',4)
xlabel('x');ylabel('y');zlabel('z');set(gca,'FontSize',20);
subplot(122);xlabel('x');ylabel('z');set(gca,'FontSize',20);
disp(['计算时间' num2str(toc) 's']);
%写入到文件
time=datestr(now,30);
print(gcf,['Simple_Mirror_3D_',time,'.eps'],'-depsc','-r600')
savefig(['Simple_Mirror_3D_',time,'.fig'])
print(gcf,['Simple_Mirror_3D_',time,'.png'],'-dpng')
disp(['耗时' num2str(toc) 's']);

得到的结果

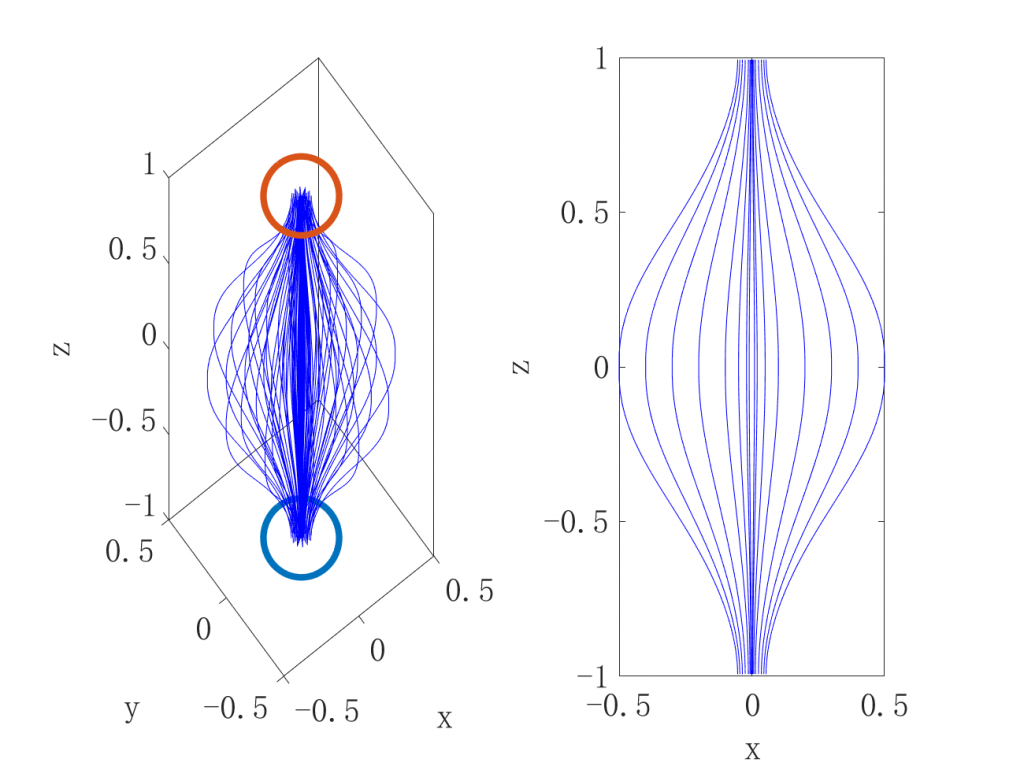
Simple_Mirror_2D.m

tic;clc;clear;
%c0:u0/2pi,I:线圈电流(A),I:线圈距离(m),R:线圈半径(m)
c0=2e-7;I=1e6;L=2;R=1.0;
n=100; x1=0;x2=6*R;z1=-1.0; z2=1.0;
dx = (x2-x1)/n; dz = 2*(z2-z1)/n;
[x,z]=meshgrid(x1:dx:x2,3*z1:dz:3*z2);
k2_1=4*R*x./((R+x).^2+(z+L/2).^2);
k2_1=k2_1-eps*(k2_1==1);
k2_2=4*R*x./((R+x).^2+(z-L/2).^2);
k2_2=k2_2-eps*(k2_2==1);
[K1,E1]= ellipke(k2_1);
[K2,E2]=ellipke(k2_2);
dd1=(R-x).^2+(z+L/2).^2;
dd1=dd1+eps*(dd1==0);
dd2=(R-x).^2+(z-L/2).^2;
dd2=dd2+eps*(dd2==0);
%线圈1产生的磁场
Bx1=c0*I*(z+L/2)./(x+eps*(x==0))./sqrt((R+x).^2+(z+L/2).^2).*((R^2+x.^2+(z+L/2).^2)./dd1.*E1-K1);
Bz1=c0*I./sqrt((R+x).^2+(z+L/2).^2).*((R^2-x.^2-(z+L/2).^2)./dd1.*E1+K1);
%线圈2产生的磁场
Bx2=c0*I*(z-L/2)./(x+eps*(x==0))./sqrt((R+x).^2+(z-L/2).^2).*((R^2+x.^2+(z-L/2).^2)./dd2.*E2-K2);
Bz2=c0*I./sqrt((R+x).^2+(z-L/2).^2).*((R^2-x.^2-(z-L/2).^2)./dd2.*E2+K2);
Bx=Bx1+Bx2;
Bz=Bz1+Bz2;
vz =[0,1]; vx=[0:0.2:4*R];
[px,pz]=meshgrid(vx,vz);
streamline(x,z,Bx,Bz,px,pz);hold on;
streamline(x,-z,Bx,-Bz,px,-pz);
streamline(-x,z,-Bx,Bz,-px,pz);
streamline(-x,-z,-Bx,-Bz,-px,-pz);
plot([-R -R R R],[z1 z2 z1 z2],'r.','markersize',40);
plot([0 0],[3*z1 3*z2],'b-','linewidth',1);
xlabel('x');ylabel('z');set(gca,'FontSize',20);
disp(['计算时间' num2str(toc) 's']);
%写入到文件
time=datestr(now,30);
print(gcf,['Simple_Mirror_2D_',time,'.eps'],'-depsc','-r600')
savefig(['Simple_Mirror_2D_',time,'.fig'])
print(gcf,['Simple_Mirror_2D_',time,'.png'],'-dpng')
disp(['耗时' num2str(toc) 's']);

得到的结果，这里线圈的半径不是0.2m，而是1.0m了。半径为0.2时画出来的图形比较难看。

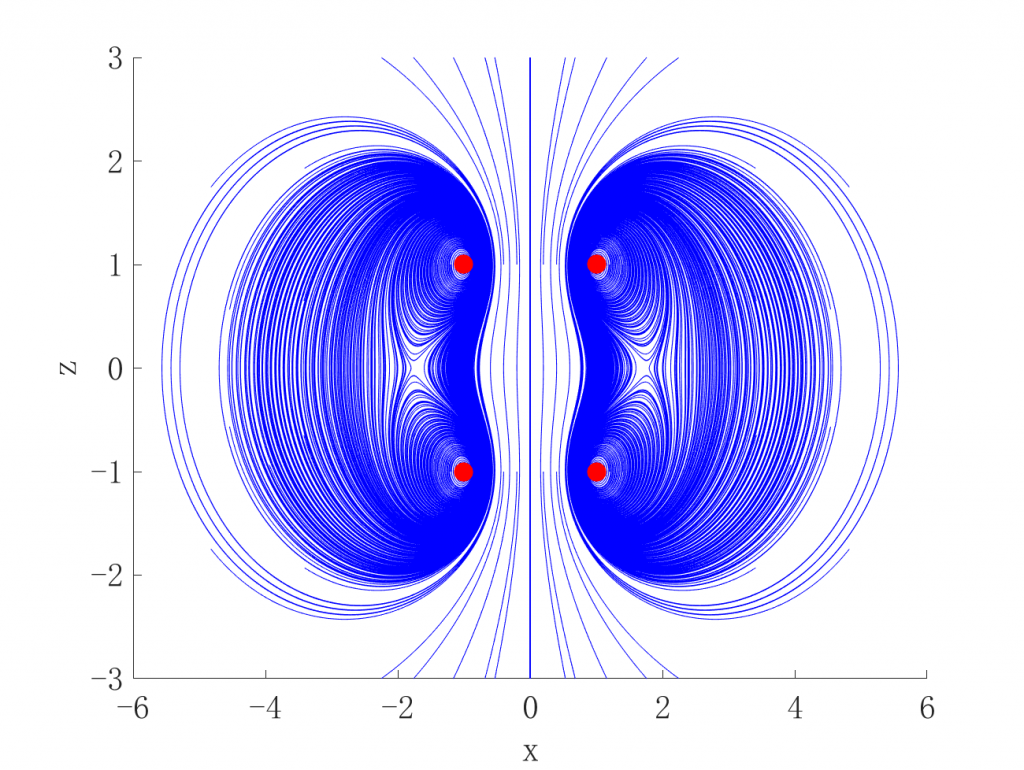
源码

欢迎转载，不需注明出处，就说是你写的